| Меню сайту |
|
 |
| Наше опитування |
|
 |
| Статистика |
Онлайн всього: 1 Гостей: 1 Користувачів: 0 |
 |
| Афоризми |
|
|
 |
| Швидкість інтернет |
Block content |
 |
| Міні-чат |
|
|
 |
|
Головна » 2016 » Вересень » 18 » Перетворення графыкыв
15:23 Перетворення графыкыв |
Тема уроку: Побудова графіків функцій за допомогою геометричних перетворень (2 уроки)

Узагальнююче повторення
У 9 класі ми навчилися за допомогою графіка функції y = f (x) будувати графіки функцій
y = f (x) + b,
y = f (x + a),
y = kf (x).
Нагадаємо правила, які дозволяють виконати такі побудови.
Графік функції y = f (x) + b можна отримати в результаті паралельного перенесення графіка функції y = f (x) на b одиниць угору, якщо b > 0, і на –b одиниць униз, якщо b < 0.
На рисунках 23, 24 показано, як працює це правило для побудови графіків функцій y = x2 – 4 і

Узагальнююче повторення
Графік функції y = f (x + a) можна отримати в результаті паралельного перенесення графіка функції y = f (x) на a одиниць уліво, якщо a > 0, і на –a одиниць управо, якщо a < 0.
На рисунках 25, 26 показано, як працює це правило для побудови графіків функцій y = (x – 2)2 і

Узагальнююче повторення
Графік функції y = kf (x) можна отримати, замінивши кожну точку графіка функції y = f (x) на точку з тією самою абсцисою і ординатою, помноженою на k.
На рисунках 27, 28, 29 показано, як працює це правило для побудови графіків функцій:
Кажуть, що графік функції y = kf (x) отримано з графіка функції y = f (x) у результаті розтягу в k разів від осі абсцис, якщо k > 1, або в результаті стиску в 1/k разів до осі абсцис, якщо 0 < k < 1.

Перетворення графіків функції
Покажемо, як можна побудувати графік функції y = f (kx), якщо відомо графік функції y = f (x).
Розглянемо випадок, коли k > 0. Якщо точка (x0; y0) належить графіку функції y = f (x), то точка належить графіку функції y = f (kx).
Отже, кожній точці (x0; y0) графіка функції y = f (x) відповідає єдина точка графіка функції y = f (kx).
Аналогічно можна показати, що кожна точка (x1; y1) графіка функції y = f (kx) є відповідною єдиній точці (kx1; y1) графіка функції y = f (x).
Тому графік функції y = f (kx), де k > 0, можна отримати, замінивши кожну точку графіка функції y = f (x) на точку з тією самою ординатою і абсцисою, поділеною на k.

Приклад
На рисунку 30 показано, як працює це правило для побудови графіків функцій:
Говорять, що графік функції y = f (kx) отримано з графіка функції y = f (x) у результаті стиску в k разів до осі ординат, якщо k > 1, або в результаті розтягу в 1/k разів від осі ординат, якщо 0 < k < 1.

Перетворення графіків
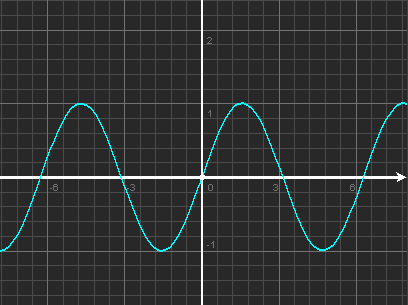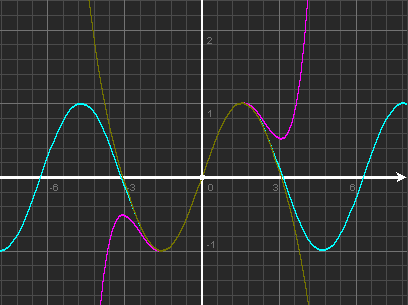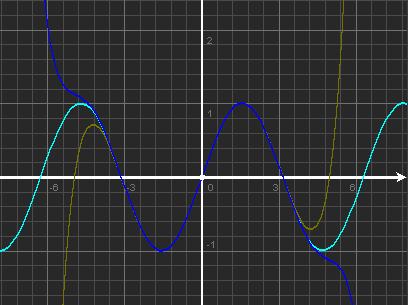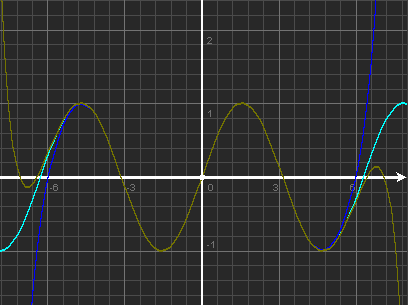
Покажемо, як побудувати графік функції y = f (–x), якщо відомо графік функції y = f (x). Зазначимо, що коли точка (x0; y0) належить графіку функції y = f (x), то точка (–x0; y0) належить графіку функції y = f (–x). Дійсно, f (–(–x0)) = f (x0) = y0. Тоді всі точки графіка функції y = f (–x) можна отримати, замінивши кожну точку графіка функції y = f (x) на точку, симетричну їй відносно осі ординат, тобто відобразивши графік функції y = f (x) симетрично відносно осі ординат.

Перетворення графіків

Приклад 1

Приклад 2

ІІ спосіб розв'язання
Первинне закріплення вивченого матеріалу
-
Як можна отримати графік функції y = f (x) + b, використовуючи графік функції y = f (x)?
-
Як можна отримати графік функції y = f (x + a), використовуючи графік функції y = f (x)?
-
Як можна отримати графік функції y = kf (x), використовуючи графік функції y = f (x)?
-
Як можна отримати графік функції y = f (kx), де k ≠ 0, використовуючи графік функції y = f (x)?

Тренувальні вправи
144.° Графік якої функції отримаємо, якщо графік функції y = x2 паралельно перенесемо:
на 5 одиниць угору;
на 8 одиниць управо;
на 10 одиниць униз;
на 6 одиниць уліво;
на 3 одиниці вправо і на 2 одиниці вниз;
на 1 одиницю вліво і на 1 одиницю вгору?

Тренувальні вправи

Тренувальні вправи

Тренувальні вправи

Робота в парах (з коментуванням)

Самостійне виконання вправи

Складання алгоритму побудови графіка функції

Закріплення вивченого матеріалу. Робота учнів біля дошки

Як побудувати графіки функцій y = f (|x|) і y =|f(x)|, якщо відомо графік функції y = f (x) ?
Як побудувати графіки функцій y = f (|x|) і y =|f(x)|, якщо відомо графік функції y = f (x) ?







Вправи

Тренувальні вправи

Домашнє завдання (розподілити самостійно на 2 уроки)
-
Читати § 5
-
Вчити алгоритми перетворення графіків функції
-
Готувати відповіді на контрольні запитання 1-4 ст. 46
-
Виконати вправи №№ 145, 146, 148, 150, 152, 155, 158, 160
-
Опрацювати приклади з поглибленого рівня рубрики “Коли зроблено уроки” (диференційовано)

|
|
Переглядів: 527 |
Додав: тома
| Рейтинг: 0.0/0 |
|
|
| Вхід на сайт |
|
 |
| Пошук |
|
 |
| Календар |
|
 |
| Архів записів |
|
 |
|