Послідовність Фібоначчі, популяризована книгою та фільмом "Код Да Вінчі" - ряд цифр, описаний у вигляді загадки італійським математиком Леонардо Пізанським, більш відомим під прізвиськом Фібоначчі, в XIII столітті.

 

Коротко сутність загадки:

Хтось помістив пару кроликів в якомусь замкнутому просторі, щоб дізнатися, скільки пар кроликів народиться при цьому протягом року. Природа кроликів така, що кожен місяць пара кроликів приводить на світ іншу пару, а здатність до народження потомства у них з'являється після досягнення двомісячного віку.

У підсумку виходить такий ряд цифр:

 

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,

 

де через кому вказано кількість пар кроликів в кожному з дванадцяти місяців. Його можна продовжувати нескінченно довго, оскільки  кожне наступне число є сумою двох попередніх.

У цьому ряді є декілька математичних особливостей.  

Він асимптотично (наближаючись все повільніше і повільніше) прагне до деякого постійного співвідношення. Однак, це співвідношення ірраціональне, тобто є числом з нескінченною, непередбачуваною послідовністю десяткових цифр у дробовій частині. Його неможливо виразити точно.

Так відношення якого-небудь члена ряду до попереднього коливається в околі числа 1,618, через pаз то перевищуючи, то не досягаючи його. Відношення до наступного аналогічно наближається до числа 0,618, що обернено пропорційно 1,618. Якщо ми будемо ділити елементи через один, то отримаємо числа 2,618 і 0,382, які так само є обернено пропорційними. Це так звані коефіцієнти Фібоначчі.

 

До чого все це? Ми наближаємося до одного з найзагадковіших явищ природи. Кмітливий Леонардо по суті не відкрив нічого нового, він просто нагадав світу про таке явище, як Золотий Перетин, яке не поступається за значимістю теоремі Піфагора.

 

 

Усі навколишні предмети ми розрізняємо в тому числі і за формою. Деякі нам подобаються більше, інші менше, ще інші зовсім відштовхують погляд. Іноді цікавість може бути продиктована життєвою ситуацією, а часом красою спостережуваного об'єкта. Симетрична і пропорційна форма сприяє найкращому зоровому сприйняттю і викликає відчуття краси та гармонії. Цілісний образ завжди складається з частин різного розміру, що знаходяться в певному співвідношенні один з одним і цілим. Золотий перетин - вищий прояв досконалості цілого і його частин в науці, мистецтві та природі.

 

Якщо на простому прикладі, то Золотий Перетин - це поділ відрізка на дві частини в такому співвідношенні, при якому більша частина відноситься до меншої, як їх сума (весь відрізок ) до більшої.

 

Але найцікавіше починається, коли ми об'єднаємо отримані знання.

 

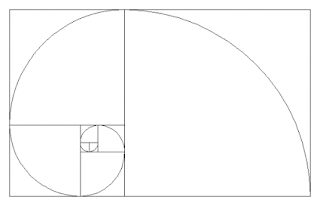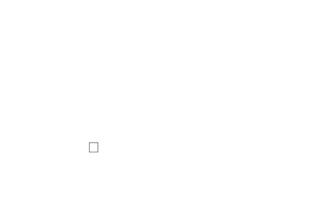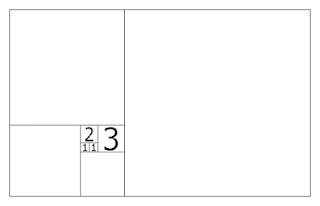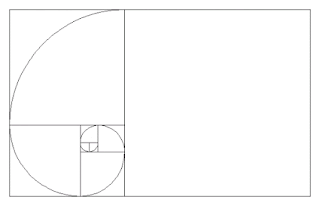
На малюнку 1 та GIF-ці наочно показано зв'язок між послідовністю Фібоначчі і Золотим перетином. Ми починаємо з двох квадратів першого розміру. Зверху додаємо квадрат другого розміру. Малюємо поруч квадрат зі стороною, яка дорівнює сумі сторін двох попередніх, третього розміру. За аналогією з'являється квадрат п'ятого розміру. І так далі поки не набридне, головне, щоб довжина сторони кожного наступного квадрата дорівнювала сумі довжин сторін двох попередніх. Ми бачимо серію прямокутників, довжини сторін, яких є числами Фібоначчі, і, як не дивно, вони називаються прямокутниками Фібоначчі.

Якщо ми проведемо плавну лінію через кути наших квадратів, то отримаємо ні що інше, як спіраль Архімеда, збільшення кроку якої завжди рівномірне.

Спіраль Архімеда та числа Фібоначчі

 

 

А якщо поглянути трохи подалі, то можна розгледіти послідовність Фібоначчі в недосяжних галактиках.

 

Звичайно, стверджувати, що всі ці явища побудовані на послідовності Фібоначчі звучить занадто голосно, але тенденція проглядається. Та й до того ж сама вона далека від досконалості, як і все в цьому світі.

 

Є припущення, що послідовність Фібоначчі - це спроба природи адаптуватися до більш фундаментальної та досконалої "золотоперетинної" логарифмічної послідовності, яка практично така ж, тільки починається з нізвідки і йде в нікуди. 

Природі ж обов'язково потрібен якийсь цілий початок, від якого можна відштовхнутися, вона не може створити щось з нічого. Відносини перших членів послідовності Фібоначчі далекі від Золотого Перетину. Але чим далі ми просуваємося по ній, тим більше ці відхилення згладжуються. Для визначення будь-якого ряду досить знати три його члена, що йдуть один за одним. Але тільки не для золотої послідовності, їй достатньо двох, вона є геометричною і арифметичною прогресією одночасно. Можна подумати, ніби вона основа для всіх інших послідовностей.

 

Кожен член золотої логарифмічної послідовності є степенем Золотої Пропорції (z). Частина ряду виглядає приблизно так:

 

... z-5; z-4; z-3; z-2; z-1; z0 ; z1 ; z2 ; z3 ; z4 ; z5 ...

 

Якщо ми округлимо значення Золотої пропорції до трьох знаків, то отримаємо z = 1,618, тоді ряд виглядає так:

 

... 0,090; 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ...

 

Кожен наступний член може бути отриманий не тільки множенням попереднього на 1,618, а й додаванням двох попередніх. Таким чином експоненціальне зростання забезпечується шляхом простого додавання двох сусідніх елементів.Це ряд без початку і кінця, і саме на нього намагається бути схожою послідовність Фібоначчі. Маючи цілком певний початок, вона прагне до ідеалу, ніколи його не досягаючи. Таке життя.

 

І все-таки, у зв'язку з усім побаченим і прочитаним, виникають цілком закономірні питання: 

Звідки взялися ці числа? 

Хто цей архітектор Всесвіту, який спробував зробити його ідеальним? 

Чи було колись все так, як він хотів? 

І якщо так, то чому не збулося? 

Мутації? 

Вільний вибір? 

Що ж буде далі? 

Спіраль скручується або розкручується?

Знайшовши відповідь на одне питання, отримаєш наступне. Розгадаєш його, отримаєш два нових. Розберешся з ними, з'явиться ще три. Вирішивши і їх, обзаведешся п'ятьма невирішеними. Потім вісьмома, потім тринадцятьма, 21, 34, 55 ...