"Персональний комп’ютер на уроці математики як засіб активізації пізнавальної діяльності учнів"

У час становлення й розвитку системи національної освіти особливо актуальними є питання вдосконалення форм, методів і технології навчання математиці в навчальних закладах різних типів.

Чи готуємо ми своїх учнів до життя в XXI столітті? А чи готові ми самі «пропускати через себе» нову інформацію, використовувати сучасні комп’ютерні і телекомунікаційні технології навчання? Потік інформації, що обрушується на наших учнів і нас самих, буде в тій мірі сприяти досягненню сучасних освітніх цілей, у якій учні навчені сприйняттю інформації і її використанню.

Педагогіка – наука соціальна, вона є гарантом розвитку суспільства, тому що те, що закладається як соціально-економічні задачі розвитку держави сьогодні, буде завтра реалізовуватися випускниками шкіл. Тому у всіх розвинутих країнах світу зроблений поворот у розвитку педагогічних технологій на навчання умінню самостійно добувати потрібну інформацію, виділяти проблеми і шукати шляхи їх раціонального розв’язання. Використання комп’ютерних технологій у навчальному процесі – один із способів включення кожного учня в освітню систему в активній позиції.

Наша школа знаходиться у складному становищі. Якщо залишити осторонь економічні проблеми, що непідвласні вчителю, то методика використання програмних продуктів у навчальному процесі, інтеграція традиційних і сучасних інформаційних технологій – це суто педагогічна проблема, розв’язання якої залежить від нас.

При цьому персональний комп'ютер може бути використаний для:

· демонстрації нових понять, фактів,

· відпрацьовування алгоритмів розв’язання різних задач;

· тренінгу, що вимагає нових знань і придбання умінь;

· самоперевірки засвоєння понять, знань;

· контролю (перевірки) якості засвоєння знань і придбаних навичок;

· творчої навчальної діяльності учнів.

Необхідний поворот від вербальних методів до інтеграції візуальних

і вербальних методів навчання. Адже давно відомо, що образна інформація засвоюється краще, ніж текстова. Мудрість, сформульована древнім китайським філософом, говорить:

«Скажи мені - і я забуду,

Покажи мені - і я запам'ятаю.

Дай мені діяти самому - і я навчуся…»

Залучення комп'ютерних технологій на різних етапах навчання допомагає реалізувати основний принцип особистісно-орієнтованого підходу в освіті – принцип діяльності. Сутність цього принципу полягає в стимуляції учнів до освітньої діяльності, що забезпечує можливості саморозвитку, самовираження і самоосвіти.

Комплексне використання різних засобів навчання сприяє створенню сприятливого пізнавального середовища. Поєднання традиційних форм і видів роботи на уроці з комп’ютерною підтримкою дає можливість максимально диференціювати та індивідуалізувати навчання, зробити процес навчання творчим, дослідницьким. Застосування інформаційних технологій дає змогу скоротити час на вивчення теми, підвищити рівень сприйняття і розуміння учнями матеріалу. Позитивний результат гарантовано, бо молодь до комп’ютерів ставиться дуже доброзичливо, вона їх любить, їм довіряє, навіть їх обожнює. І треба розумно використати це ставлення школярів до комп’ютера при плануванні навчального процесу.

Важливі також деякі психологічні аспекти висвітлюваної теми. Учні мають різний психологічний статус і багато хто з них хворобливо ставиться до зауважень, дуже боїться зазнати фіаско на очах у класу. У діалозі з комп'ютером нічого подібного не відбувається: комп'ютер не рахує, скільки було невдалих спроб розв’язання задачі, не робить ніяких зауважень. Він ще й підкаже, що і як потрібно зробити. Таким чином формується ситуація психологічного комфорту, яка створює можливість пізнавального та емоційного розкріпачення учнів.

У діючій програмі по математиці рекомендоване використання персонального комп'ютера як контролюючої машини, навчального тренажера, моделюючого стенда, інформаційно-довідникової системи, ігрового навчального середовища, електронного конструктора, експертної системи. Використання комп'ютера під час вивчення математики дає наочні уявлення про досліджувані поняття, закономірності, функції, геометричні фігури, що сприяє розвитку образного мислення учнів.

На перших уроках з теми “Розв’язання квадратного рівняння за формулою його коренів” у 8 класі з метою формування умінь та навичок застосування формули коренів квадратного рівняння підручники пропонують розв’язати понад 50 рівнянь. Активізувати дію мотиваційних чинників у створенні позитивного ставлення до виконання такої одноманітної, але такої потрібної роботи допоможе вчителю програма “Математический помощник”, що виконуватиме роль навчального тренажера. Учні в зошитах за формулою знаходять корені квадратного рівняння, уводять значення коефіцієнтів a,b,c у відповідні поля інформації, отримують на екрані монітора корені даного рівняння, порівнюють з тими, що записані в зошиті. Для перших 5-6 рівнянь значення коефіцієнтів a, b, c доцільно голосно прокоментувати. На певному етапі цієї роботи можна запропонувати учням зібрати “колекцію помилок” Для цього у тому випадку, коли корені рівняння у зошиті не співпадають з коренями на екрані монітора, учень знаходить помилку, аналізує причини, що призвели до неї, і фіксує їх на полях зошита. По закінченні даного етапу уроку усі помилки класифікуються вчителем, самі учні дають рекомендації щодо запобіганню появи кожної конкретної помилки, виходячи з причин її появи.

Аналогічним чином можна організувати роботу по формуванню умінь та навичок знаходження кількості сполучень з a елементів по b у 9 класі.

Із задоволенням виконують учні усну контрольну роботу, провести і перевірити яку допомагає персональний комп’ютер. Даний підхід до використання комп'ютерних технологій сприяє тому, що учень стає суб'єктом своєї пізнавальної діяльності. З іншого боку, перед учителем відкриваються широкі можливості в забезпеченні своєчасної перевірки й обліку навчальних досягнень учнів. Отже, підвищується зацікавленість школярів у пізнавальній діяльності, формується їхнє свідоме ставлення до навчання, адекватна самооцінка, збільшується щільність навчальної діяльності. Робота складена у формі тестів. Учні повинні тільки ввести отриманий результат у комп’ютер. І у разі успіху, і у разі помилки комп’ютер відразу повідомляє вірну відповідь. Таким чином учень має можливість проаналізувати свої помилки. Під час виконання роботи можна робити деякі необхідні записи, а якщо це – контрольна робота з геометрії, то малюнки є необхідними. Результат навчальної діяльності буде відомий учню і вчителю відразу по закінченні роботи з даною програмою.

На прикладі теми “Властивості функцій”(9 клас, поглиблене вивчення математики) показано можливості використання комп'ютерних технологій на різних етапах уроку з різними цілями. На етапі актуалізації знань для перевірки домашнього завдання, на етапі пояснення нового матеріалу з метою створення умов для розв’язання проблемної ситуації шляхом експерименту, для самостійного “відкриття” знань, підтвердження власних гіпотез, на етапі закріплення знань і умінь для самоконтролю, створення ситуації успіху, на етапі систематизації й узагальнення знань для наочності та стимулювання творчості.

І. Після введення понять парності та непарності функцій учням пропонуються вправи на закріплення:

1. Дослідити функції на парність і непарність (робота на дошці):

1) f(x)= 3х⁴–х²+5

 2) f(x)= –3х⁶

 3) f(x)= х⁵+2х

4) f(x)=

5) f(x)= –4х

 6) f(x)=

 7) f(x)= 0,5х–3

8) f(x)= х²+6х+1

2. Побудувати графіки даних функцій за допомогою комп’ютерної програми Edvanced Grapher.

8 учнів (за бажанням) будують графіки даних функцій на комп’ютерах.

Висновки:

1) Графік будь-якої парної функції симетричний відносно осі ординат.

2) Знання того, що функція парна чи непарна, спрощує побудову графіка функції.

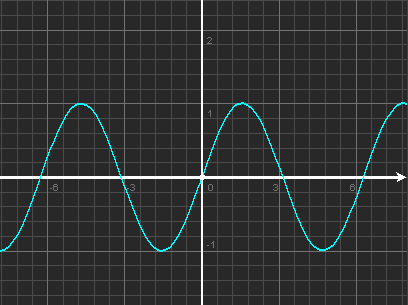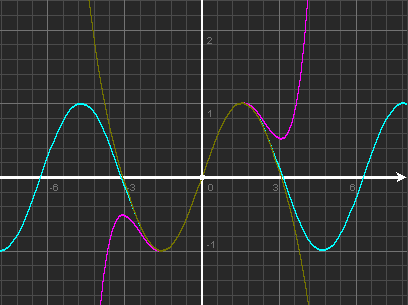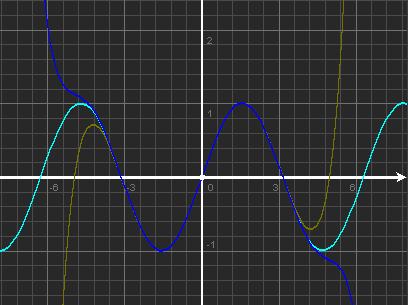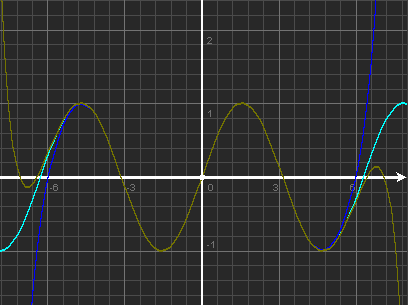
3. Побудувати графік функції .

Як будували такий графік у 8 класі?

Спробуємо ще один спосіб побудови графіка:

1) дослідимо функцію на парність;

2) побудуємо її графік для :

3) отриману частину графіка відобразимо симетрично відносно осі Оу;

Перевіримо за допомогою програми Advanced Grapher,

Перевіримо, чи вірно ми побудували графік.

IІ. Одним із завдань додому було задати формулою яку-небудь парну функцію. Під час перевірки домашнього завдання учням пропонується сісти за комп’ютер, ввести функцію в поле “Формула” для побудови графіка “своєї” функції за допомогою програми “Advanced Grapher”. Якщо графік є симетричним відносно осі Оу, то формула складена вірно.

ІІІ. Задовго до уроку один із учнів отримав творче завдання: самостійно вивчити тему “Найпростіші перетворення графіків функцій” і оформити висвітлення даного питання за допомогою майстра презентацій Power Point пакета Microsoft Office 2000. Для активізації сприйняття інформації використовуються елементи анімації.

Пояснення нового матеріалу учнем проводилось за такою схемою:

1) порівняти розташування графіків функцій

а) , ,

б) , , ;

2) зробити відповідні висновки;

3) свою гіпотезу перевірити з графіком функції ;

4) записати у зошит алгоритм перетворення за допомогою умовних позначень.

Звичайно, якість засвоєння програмного матеріалу забезпечується не тільки використанням комп'ютерних технологій, а й інтеграцією їх із традиційними методами навчання. І дуже важливо, щоб ця інтеграція сприяла формуванню вільної творчої особистості учня.